En la topografía, los mapas deben ser creados con curvas de nivel, curvas maestras, símbolos convencionales, escalas, etc. Son estas características, en conjunto, las capaces de recrear la visión completa de una parcela.
Gracias a ellas, podemos visualizar los problemas de cada terreno, así como los datos más relevantes de este. Todas estas herramientas son importantes para encarnar un espacio, siendo las curvas de nivel base fundamental para ello. Es un instrumento que guiará la creación desde el primer punto.
Pero, ¿por qué es importante o siquiera relevante para la topografía este tipo de trazo? La respuesta es simple, pero detrás posee un sinfín de datos y trabajo. Gracias a estas líneas, que se adaptan a los rasgos sinuosos, se nos otorgarán los números para cálculos, las variantes de terreno, entre otras tantas cosas.
Por ello, es importante conocer e implementar las curvas de forma idónea, y en el siguiente artículo se brindará un panorama completo sobre esta útil y fundamental herramienta topográfica.

Table of Contents
¿Qué son las curvas de nivel?
En términos simples, las curvas de nivel son un conjunto de líneas encargados de conectar puntos, estos conectan a una misma altura. Generalmente, estas líneas se encuentran presentando una igualdad de condiciones concreta, lo cual permite mostrar e identificar los distintos niveles y formas encontrados en cualquier escenario.
Asimismo, estas son muy empleadas al momento de representar formas tridimensionales en los espacios bidimensionales. Resultan sumamente relevantes para la topografía, sobre todo para las cartas de esta índole. Porque son referencias que proveen información cuantitativa de los espacios, específicamente en su relieve.
Esta técnica puede ser complementada con sombreado o coloreo en los espacios, facilitando su lectura terrenal y logrando entendimiento del conjunto. También destaca que esta herramienta es capaz de visibilizar, de modo general y descriptivo, el perfil, inclinación y elevación de la tierra.
Este método también es uno de los más prácticos a la hora de representar las distintas elevaciones en una superficie específica. Haciéndolas incluso más fáciles de comprender que en el propio espacio.
Características de esta técnica
Hay factores que deben tenerse en consideración a la hora de utilizar curvas de nivel en el armado de un plano, algunas de ellas son:
- Son líneas cerradas. También deben ser paralelas entre sí.
- Cada punto en el plano debe tener la misma cota.
- Su trazo es regular y uniforme; no se cortan a menos que se deba indicar anomalía.
- La equidistancia es un valor absoluto que debe ser constante en todo el plano.
- No se dividen.
- Se hacen más gruesas los arcos de nivel que sean múltiplo de 10. Esto con el objetivo de facilitar la búsqueda de un punto.
- Cuando la parcela tenga un espacio convexo hacia abajo, debe representarse con el formato U.
- Las áreas de drenaje deben ser representadas con una figura que mantenga su vértice hacía arriba, es decir con una V.
- La cohesión de 2 crestas se muestra con una que emule una M.
- Se debe indicar siempre la elevación de cada curva de nivel; para ello, se interrumpe la curva para señalar esta con un número.
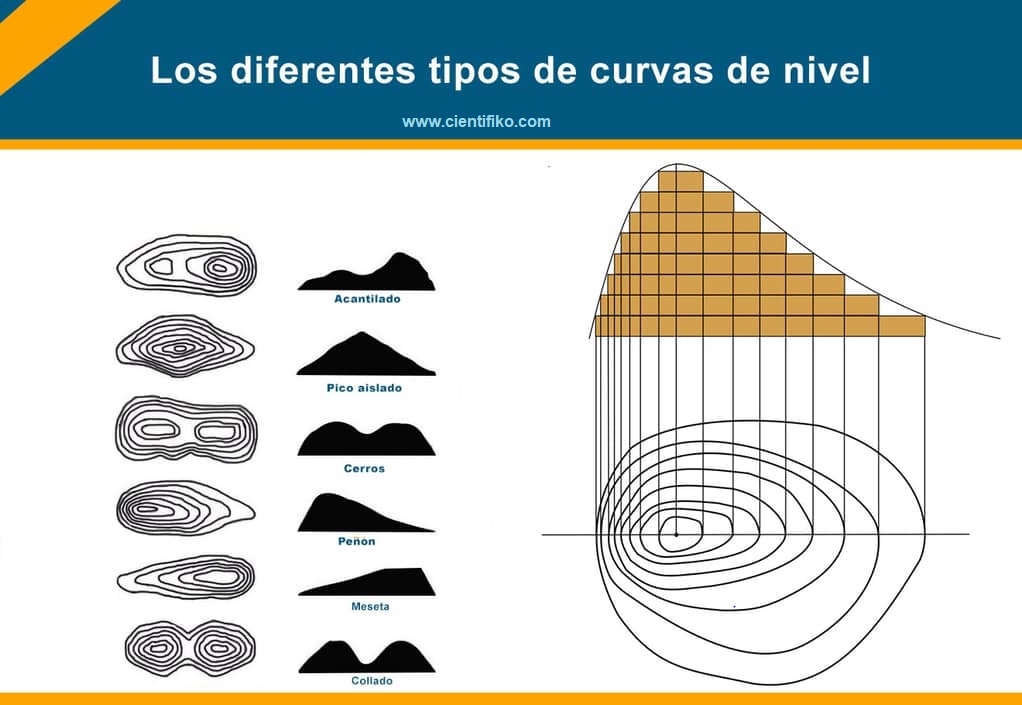
Tipos de curva de nivel
No existe solo un estilo de curva de nivel. En su trazado o uso, podemos encontrar distintas formas de aprovechar las curvas en el mapa. Con ello, esta herramienta nos facilita ciertos cálculos y trazos. Es por eso que pueden clasificarse en distintos tipos según su utilidad, como lo son:
· Maestra
También conocida como principal, se tratan de arcos encargados de simplificar la lectura del esbozo. Se dibujan en constante diferencia de elevación, a intervalos iguales; se representan con líneas gruesas y continúas.
· Intermedia
Esta simboliza a un valor unitario constante en medio de dos arcos principales. Por ello, su intervalo depende solo de las curvas principales. Debe esbozarse en el mapa con un trazo delgado y continuo.
· Suplementaria
Llamada algunas veces auxiliar, esta curva se utiliza para figurar un relieve que resulte de interés y que, por un motivo u otro, la equidistancia establecida no lo alcance.
· Isóbatas
Son aquellas que se emplean en la representación de los cuerpos de agua. Todas sus líneas unen los puntos que poseen igual profundidad.
· De configuración
Se usa para imitar el relieve del terreno, centrándose en evocar la forma de este de manera idónea. Es una curva que produce aproximaciones, por lo que no se debe utilizar la numeración de la altitud. Pues no existe un respaldo que sustente el número, solo es una representación.
· Dudosa
Es aquella curva que representa datos que aún son dudosos.
· Intercalada
Es la que se debe emplear cuando existe una separación muy amplia entre una curvatura y otra. Esta curva de nivel permite que la representación cartográfica sea más fiel al terreno en cuestión.
· Depresión
Se trata de un diagrama formado por distintas curvas, el cual se utiliza para representar un valor intermedio entre las pendientes que se ubican en el espacio. Las elevaciones son su única fuente de información.
· Clinográfica
Se trata de un diagrama formado por distintas curvas, el cual se utiliza para representar un valor intermedio entre las pendientes que se ubican en el espacio. Las elevaciones son su única fuente de información.
· De pendiente
Diagrama que simboliza las diversas inclinaciones que nacen de las distancias existentes entre cada una de las curvas de nivel en la carta.
· Hipsométrica
Es un diagrama de curvas que reproduce la dimensión de las superficies con lagunas. Se debe tomar en consideración que su eje principal siempre representa la altura de dicho terreno.
Intervalos entre las curvas de nivel
Puede definirse como la distancia vertical de una comba a otra. En este sentido, se puede entender que entre más intervalo exista, menos curvas habrá. Por el contrario, si se disminuye el intervalo, existirán más curvas. Es decir, el intervalo es el trecho de una curva a otra, que a su vez mide la cantidad de arcos que tiene un solar o carta.
Es por ello que los mapas de escalas pequeñas utilizan, por lo general, intervalos de 50 o 100 metros. Por otro lado, para los planos que necesiten mayores datos sobre y del espacio, se utilizan intervalos de 5, 2, y 0.50 m.
Es la razón por la que no se debe olvidar que el intervalo entre curvas depende de costos, los rasgos de la tierra, la precisión y la legibilidad del plano.
Además, debe mantenerse el mismo intervalo elegido durante la realización de todo el dibujo; de lo contrario, se generarán errores: más de un intervalo dentro del plano lleva a errores de interpretación.
Significados de las curvas
Cada curva de nivel ayuda a formar el panorama completo del terreno. Con ellas se revelan características específicas y definidas de cada espacio, es por ello que es necesario conocerlas para lograr una interpretación idónea de las curvas.
- Las curvas con un espacio uniforme entre ellas indican exactamente eso: que la pendiente es uniforme.
- Aquellas curvas que están muy cerca la una de la otra en la mayor elevación del terreno, pero que están más separados en las partes más bajas, simbolizan a una pendiente que es cóncava.
- Por otra parte, cuando el espacio es mayor en la elevación más alta de la pendiente y menor en el nivel inferior, la pendiente es convexa.
- Las curvas más altas de los riscos y las más bajas de los valles van parejas.
- Nunca pueden ni deben cruzarse.
- Solo existe una variante que se considera excepción a la regla anterior: que exista un sobrevolado o un acantilado vertical en el solar.
Cuáles son las aplicaciones que tienen este tipo de herramienta
Además de generar una representación gráfica y completa de la parcela y el relieve que hay dentro de esta, las curvas poseen otras aplicaciones para las que pueden resultar muy útiles. Gracias a ello, son sumamente relevantes para las obras civiles, la planificación, usos agrícolas, etc.
Con una carta que posea curvas de nivel se puede precisar la elevación desde y de cualquier lugar en el plano, así como lograr la estimación de los volúmenes de corte, encontrar la inclinación dentro de dos puntos, entre otros. Estas líneas con forma arqueada tienen infinidad de usos en la preparación y construcción de proyectos. Varios de los modos más fundamentales para emplear las curvas son:
Cálculo de Pendientes
La pendiente que está entre dos arcos de nivel que son contiguos; debe ser igual con relación al intervalo de la equidistancia y a la distancia longitudinal que los aleja a ambos. La fórmula para lograr este cálculo es la siguiente:
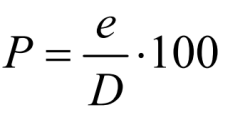
Donde P es la pendiente del terreno en porcentaje, “e” es la equidistancia entre una curva y otra, mientras que “D” encarna la distancia existente de un punto al otro.
Hay que acotar que, la razón de que la distancia siempre sea horizontal, es porque la carta vista desde arriba está en ese enfoque.
Trazados de líneas de pendiente constante
Se utiliza para escoger la ruta donde se va a ubicar la carretera dentro de un espacio sinuoso u ondulado, conocido coloquialmente como terreno montañoso. Es sumamente importante para los proyectos viales, de riego, de construcción, etc.
Sin importar qué tipo de carretera se elija, se necesita trazar una línea de pendiente constante que mantenga, dentro del límite de inclinación máxima, a los vehículos pesados. Tomando en cuenta su comportamiento y, por supuesto, el terreno.
Hay que tener en consideración que, distintos factores como lo son el costo de tierra, factores geomorfológicos y ambientales, entre otros; influyen en la elección de la vía definitiva.
Cálculo de la cota de un punto
En los proyectos es común determinar la cota desde algún punto sobre un mapa que tiene curvas. El procedimiento que hay que seguir para el cálculo es el siguiente:
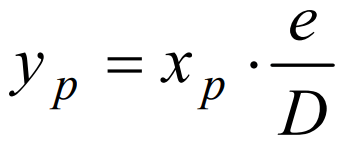
- Se traza por la pendiente (P) un arco, nacido de un círculo, que sea tangente a la curva que tenga mayor elevación, estableciendo A.
- Hay que unir A con P, y prolongar ese alineamiento hasta que se corte la curva inferior, logrando así determinar B.
- Se miden las distancias horizontales P-B, siendo esta xp, y A-B, siendo esta D.
- Gracias a la equidistancia (e), se puede calcular yp:
- La cota P es aquella que se forma con la cota B+Yp
Topografía modificada
Las curvas de nivel contribuyen a las elaboraciones de planos de la topografía modificada. Esta es una representación gráfica del proyecto implementado sobre la zona en la que se planea construir dicha obra. Es una estrategia común en la arquitectura, sobre todo en el urbanismo, y en ingeniería.
Este plano permite que se vea el resultado del diseño final para sus modificaciones y se ubiquen espacios como el drenaje. Así como, medir los movimientos de tierra, las alteraciones en el espacio, etc.
Beneficios del empleo de curvas de nivel
En pocas palabras, las curvas de nivel resultan totalmente beneficiosas para el armado de planos, mapas y todo tipo de objeto que necesite un modelado 2D de un solar. Con su ayuda, cada detalle que se encuentre dentro del trecho de tierra elegido es tomado en cuenta.
Presta sus líneas para cada elemento dentro del espacio a representar, sin resultar agobiante o molesto. Evita que el dibujo esté cargado, complementando sus datos a través de números. Además, facilita que se encuentren los puntos con los que se desea trabajar.
A su vez, participan activamente en los cálculos que se necesiten para abrir camino en los solares. También, para crear espacios para los edificios, sembradíos y otras tantas actividades, que requieran manipulación o trabajo de tierra.
Conclusión
Pese a las actualizaciones tecnológicas que facilitan la construcción y la creación de planos, las curvas de nivel continúan teniendo un papel indispensable para el desempeño de actividades donde deba manipularse la tierra. De hecho, los nuevos modelos para la creación de planos tienen su propio apartado para el agregado de curvas.
No se puede olvidar que es fácil de adaptar, pues no hay reglas que impidan que su trazo sea curvo, recto o zigzagueante. Asimismo, puede dibujar cada tipo de parcela, permitiendo que se representen depresiones, elevaciones y hasta cuerpos de agua.
Es, entonces, un instrumento completamente útil para construcción de una carta sin importar el trazo o la dificultad del campo. Por ello es importante dentro de la arquitectura, topografía, matemáticas y el avance en general.
Referencias
http://www.edeca.una.ac.cr/images/AplicTop2020/Curvas_de_nivel.pdf
https://sjnavarro.files.wordpress.com/2008/08/folleto-topografia-ii.pdf
https://toposena.files.wordpress.com/2011/07/cap9-curvas-nivel.pdf
http://webdelprofesor.ula.ve/forestal/zamora/dcweb/curvas%20de%20nivel.htm













0 comentarios